QT+C++实现连连看
需求简单分析。
玩过连连看的都知道,连连看其实就是测试能不能用少于等于3条相连的线,连接两个点(图片)。线的条数为0~3条。
先只实现了逻辑,并做了智能测试,程序自己可以演示玩连连看的过程,界面还没有做,准备用QT(不熟),
0条线表示两个点相邻,在坐标轴上看就是X轴相同,Y轴值相差1,或是Y轴相同X轴值相差1。
1条线表示两个点同X或是同Y轴,且两点之间没有其他点。
2条线表示两个点确定的长方形,存在连接两个点的两边上都没有其他任何点
3条线复杂点,经过反复的思考,决定将3条线的情况分成5类:上下左右中(东南西北中)。这样的分类主要是想让代码更好理解,思路看起来更简单点。
上:连接两个点的3条线的第二条线在两个点的上面
下: 下
左: 左
右: 右
中:连接两个点的线在这两个点确定的长方体内(包括长方体的边)
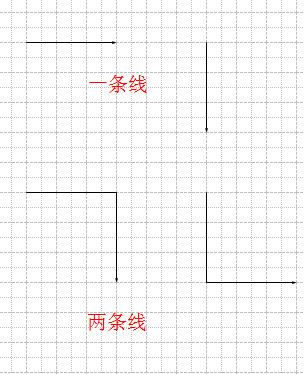
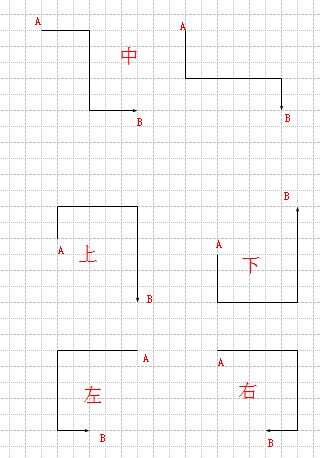
所有的情况都包括在0~3条线的情况中,实现这三种情况,连连看的最主要功能就算是实现了。在实现方面用得最多的就是判断两个点是否在同一条直线上,且直线上没有其他点,两条线和三条线的情况都可以转化成两组或是三组两个点是否在同一条直线上的问题。
在实现上,我用了一个二维数组A[row][column]来标示某个点上是否有图片,且这两个点是否是同一种图片,0表示没有图片,其他值表示有图片,如果两个点的值相同表示是相同的图片,然后我们就至于要测试这两个点是否想通了。所有的实现都是基于这个二维数组A的。在这一版里,我主要是实现了所有的逻辑,没有做界面,界面准备用QT实现,但由于我跟QT还不熟,所以还得等一段时间,先实现了大致的逻辑,并模拟了连连看的过程,模拟的过程发现了一些错误,但最后也证明我的实现是正确的,也没有任何性能问题,当然也跟连连看的特殊有关,因为连连看的最主要的功能其实就是测试两个点是否能连接成功,而判断指令对于计算机来说执行是非常快的。
拐点:最多有3条线,最多也就两个拐点,知道了端点及拐点,我就知道连接两个点的线了。
判断是否成功:开始的时候记下点的个数,每成功连接两个点,点的个数就减2,点的剩余个数为0时就是成功了,当然也可以每次都扫描一次看剩余的点数是否大于0,个人认为用一个变量记下剩余的点的个数会快些。
判断是否无解:如果没有两个点能够相连,就表示无解了。实现这个功能同样有两种方式。方法一是每次判断是否无解时都扫描一次,看是否存在两个点能够相连,存在表示有解,否则表示无解。方法二是完整的扫描一次,记下能够相连的点对数,没成功相连一次,就让这个数减一,当然不一定是减一,可能是减二,也可能是增一增二,至于为什么是这样大家应该知道,在这里我采取的是减一,如果相连的点的对数小于1时就在扫描一次,我们就得到了剩余能够相连的点对的个数,如果还是小于1,表示无解。
实现的简单解释
Point表示坐标轴上的一个点,所有的实现都是基于点的概念,用户点击的图片或者说是按钮都表示一个点,而一个点就是两个坐标X轴和Y轴,并附带了一些其他的辅助方法。
#pragma once//表示坐标轴上的一个点[X,Y]struct Point{ Point():X(-1),Y(-1){} Point(int _x,int _y):X(_x),Y(_y){} Point(const Point& p):X(p.X),Y(p.Y){} Point& operator=(const Point& p){ X=p.X; Y=p.Y; return *this; } inline bool operator==(const Point& p) { return X==p.X && Y==p.Y; } inline bool operator==(Point& p) { return X==p.X && Y==p.Y; } inline bool operator!=(const Point& p) { return X!=p.X || Y!=p.Y; } inline bool operator!=(Point& p) { return X!=p.X || Y!=p.Y; } int X;//X轴 int Y;//Y轴}; TwoPoint其实是对两个点的一层简单的包装。用户需要点击两个点,我就用这个类来包装这两个点,连接两个点,最多可能出现2两个拐点(在需要三条线连接两个点的时候),我们还是可以用TwoPoint来包装这两个拐点,并附带了一些其他的辅助方法。
#pragma once//用于记录用户点击了哪两个点 class TwoPoint{ public: TwoPoint(); ~TwoPoint(); //添加点 bool AddPoint(const Point& p); //点的个数 int Count() const; Point First() const; void First(const Point& p); Point Second() const; void Sort(); void Clear(); private: TwoPoint(const TwoPoint& p); TwoPoint& operator=(const TwoPoint& p); Point* first; Point* second; int count;}; PathRecord将用户点击的两个点及拐点,按顺序连接起来经过的所有的点集合,开始在做的时候主要是为了测试用的。
#pragma once//存放连线经过的所有点class PathRecord{ public: //清除集合中所有的元素 void Clear(); void AddPoint(const Point& p);//添加一个点 void AddPointLine(const Point& first,const Point& second);//添加两个点确定的直线上所有的点 void AddPoint(const Point& first,const Point& center1,const Point& second); void AddPoint(const Point& first,const Point& center1,const Point& center2,const Point& second); ~PathRecord(); Point* operator[](int index); int Size(); private: vector pointVector;}; PathFind主要是测试两个点是否能成功连接,连连看的核心实现就是他了。
#pragma once extern DType A[row][column];//寻路,主要的逻辑实现 class PathFind{ public: PathFind(); ~PathFind(); bool Left(const Point& first,const Point& second); bool Right(const Point& first,const Point& second); bool Top(const Point& first,const Point& second); bool Bottom(const Point& first,const Point& second); bool Center(const Point& first,const Point& second); bool OneLine(TwoPoint& endPoint); bool OneLine(const Point& first,const Point& second); bool MoreLine(TwoPoint& endPoint); bool MoreLine(const Point& first,const Point& second); bool Near(TwoPoint& endPoint); bool Near(const Point& first,const Point& second); bool Search(TwoPoint& endPoint); bool Search(const Point& first,const Point& second); private: //判断两个点是否在一条竖线上即同Y bool SameY(const Point& first,const Point& second); //判断两次点击是否在一条横线上即同X bool SameX(const Point& first,const Point& second); }; CheckResult判断是否成功或是无解。
#pragma once //结果判定-判定是死局或是已通关class CheckResult{ public: CheckResult(); CheckResult(int _leftPoint); int LeftPoint() const;//返回剩下的点 int LeftLinkLine();//可连接的点对数 void SearchLeftLinkLine();//查询可连接的点对数 void SearchLeftPoint();//查询剩下的点个数 bool Reduce2Point();//减少两个剩余的点 bool IsSuccess();//判断是否成功 bool IsNoSolution();//是否是无解 private: int leftPoint;//剩下的点用于判断是否结束 volatile int leftLinkLine;//可连接的点对数 用于判断是否死局 }; IntelligentTest智能测试,就是让电脑来玩连连看,事实证明电脑玩得很快啊,主要是用来测试的,经过他的测试就知道程序实现是否有问题了。这也是很关键的一个环节,测试发现了一些问题,这也是我少有的写测试相关的代码,个人认为自己写测试代码比手动测试效果好很多啊。
#pragma once//智能测试class IntelligentTest{ public: IntelligentTest(); void Remove(const Point& p);//删除已经连接成功的点 Point GetFirstPoint();//获取第一个点 Point GetSecondPoint();//获取第二个点 void AddHasReadPoint(const Point& p);//将已经检索过得点(暂时没有找到跟他匹配的点)加入hasReadList中 private: void InitDataBind();//将所有非空的点的坐标(某个值)加入集合noReadList中 int firstIndex;//第一个点在集合中的索引 int secondIndex;//第二个点在集合中的索引 vector hasReadList;//存放已经读了的点信息 vector noReadList;//存放剩下的点信息}; 开始图形及运行时间如下:
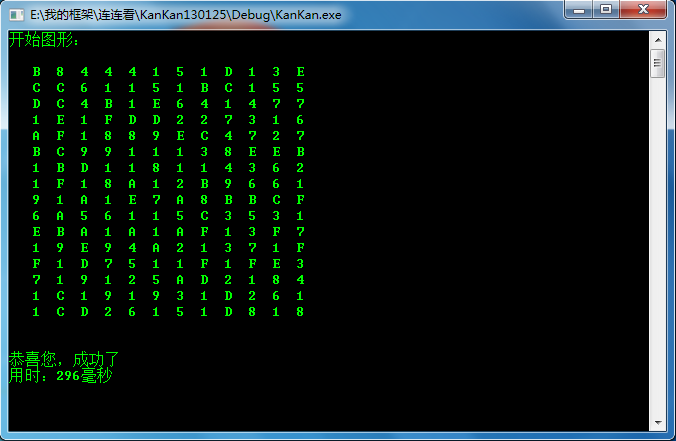
智能测试,程序自动玩连连看步骤如下:
步骤1:(1,1)~(6,1) -> B X 8 4 4 4 1 5 1 D 1 3 E C C 6 1 1 5 1 B C 1 5 5 D C 4 B 1 E 6 4 1 4 7 7 1 E 1 F D D 2 2 7 3 1 6 A F 1 8 8 9 E C 4 7 2 7 X C 9 9 1 1 1 3 8 E E B 1 B D 1 1 8 1 1 4 3 6 2 1 F 1 8 A 1 2 B 9 6 6 1 9 1 A 1 E 7 A 8 B B C F 6 A 5 6 1 1 5 C 3 5 3 1 E B A 1 A 1 A F 1 3 F 7 1 9 E 9 4 A 2 1 3 7 1 F F 1 D 7 5 1 1 F 1 F E 3 7 1 9 1 2 5 A D 2 1 8 4 1 C 1 9 1 9 3 1 D 2 6 1 1 C D 2 6 1 5 1 D 8 1 8 步骤2:(1,3)~(1,4) -> 4 8 X X 4 1 5 1 D 1 3 E C C 6 1 1 5 1 B C 1 5 5 D C 4 B 1 E 6 4 1 4 7 7 1 E 1 F D D 2 2 7 3 1 6 A F 1 8 8 9 E C 4 7 2 7 C 9 9 1 1 1 3 8 E E B 1 B D 1 1 8 1 1 4 3 6 2 1 F 1 8 A 1 2 B 9 6 6 1 9 1 A 1 E 7 A 8 B B C F 6 A 5 6 1 1 5 C 3 5 3 1 E B A 1 A 1 A F 1 3 F 7 1 9 E 9 4 A 2 1 3 7 1 F F 1 D 7 5 1 1 F 1 F E 3 7 1 9 1 2 5 A D 2 1 8 4 1 C 1 9 1 9 3 1 D 2 6 1 1 C D 2 6 1 5 1 D 8 1 8 步骤3:(2,1)~(6,2) -> C 8 4 1 5 1 D 1 3 E X C 6 1 1 5 1 B C 1 5 5 D C 4 B 1 E 6 4 1 4 7 7 1 E 1 F D D 2 2 7 3 1 6 A F 1 8 8 9 E C 4 7 2 7 X 9 9 1 1 1 3 8 E E B 1 B D 1 1 8 1 1 4 3 6 2 1 F 1 8 A 1 2 B 9 6 6 1 9 1 A 1 E 7 A 8 B B C F 6 A 5 6 1 1 5 C 3 5 3 1 E B A 1 A 1 A F 1 3 F 7 1 9 E 9 4 A 2 1 3 7 1 F F 1 D 7 5 1 1 F 1 F E 3 7 1 9 1 2 5 A D 2 1 8 4 1 C 1 9 1 9 3 1 D 2 6 1 1 C D 2 6 1 5 1 D 8 1 8 步骤4:(2,2)~(3,2) -> C 8 4 1 5 1 D 1 3 E X 6 1 1 5 1 B C 1 5 5 D X 4 B 1 E 6 4 1 4 7 7 1 E 1 F D D 2 2 7 3 1 6 A F 1 8 8 9 E C 4 7 2 7 9 9 1 1 1 3 8 E E B 1 B D 1 1 8 1 1 4 3 6 2 1 F 1 8 A 1 2 B 9 6 6 1 9 1 A 1 E 7 A 8 B B C F 6 A 5 6 1 1 5 C 3 5 3 1 E B A 1 A 1 A F 1 3 F 7 1 9 E 9 4 A 2 1 3 7 1 F F 1 D 7 5 1 1 F 1 F E 3 7 1 9 1 2 5 A D 2 1 8 4 1 C 1 9 1 9 3 1 D 2 6 1 1 C D 2 6 1 5 1 D 8 1 8 步骤5:(2,4)~(1,6) -> 1 8 4 X 5 1 D 1 3 E 6 X 1 5 1 B C 1 5 5 D 4 B 1 E 6 4 1 4 7 7 1 E 1 F D D 2 2 7 3 1 6 A F 1 8 8 9 E C 4 7 2 7 9 9 1 1 1 3 8 E E B 1 B D 1 1 8 1 1 4 3 6 2 1 F 1 8 A 1 2 B 9 6 6 1 9 1 A 1 E 7 A 8 B B C F 6 A 5 6 1 1 5 C 3 5 3 1 E B A 1 A 1 A F 1 3 F 7 1 9 E 9 4 A 2 1 3 7 1 F F 1 D 7 5 1 1 F 1 F E 3 7 1 9 1 2 5 A D 2 1 8 4 1 C 1 9 1 9 3 1 D 2 6 1 1 C D 2 6 1 5 1 D 8 1 8